
Applets
contents
visual index
 introduction
introduction std_logic_1164
std_logic_1164 gatelevel circuits
gatelevel circuits delay models
delay models
 gate vs. wir...
gate vs. wir...
 gate delay d...
gate delay d...
 ring oscillator
ring oscillator
 hazards
hazards
 NAND-chain
NAND-chain
 D-flipflop h...
D-flipflop h...
 clock-doubler
clock-doubler
 2-phase cloc...
2-phase cloc... flipflops
flipflops adders and arithm...
adders and arithm... counters
counters LFSR and selftest
LFSR and selftest memories
memories programmable logic
programmable logic state-machine editor
state-machine editor misc. demos
misc. demos I/O and displays
I/O and displays DCF-77 clock
DCF-77 clock relays (switch-le...
relays (switch-le... CMOS circuits (sw...
CMOS circuits (sw... RTLIB logic
RTLIB logic RTLIB registers
RTLIB registers Prima processor
Prima processor D*CORE
D*CORE MicroJava
MicroJava Pic16 cosimulation
Pic16 cosimulation Mips R3000 cosimu...
Mips R3000 cosimu... Intel MCS4 (i4004)
Intel MCS4 (i4004) image processing ...
image processing ... [Sch04] Codeumsetzer
[Sch04] Codeumsetzer [Sch04] Addierer
[Sch04] Addierer [Sch04] Flipflops
[Sch04] Flipflops [Sch04] Schaltwerke
[Sch04] Schaltwerke [Sch04] RALU, Min...
[Sch04] RALU, Min... [Fer05] State-Mac...
[Fer05] State-Mac... [Fer05] PIC16F84/...
[Fer05] PIC16F84/... [Fer05] Miscellan...
[Fer05] Miscellan... [Fer05] Femtojava
[Fer05] Femtojava FreeTTS
FreeTTS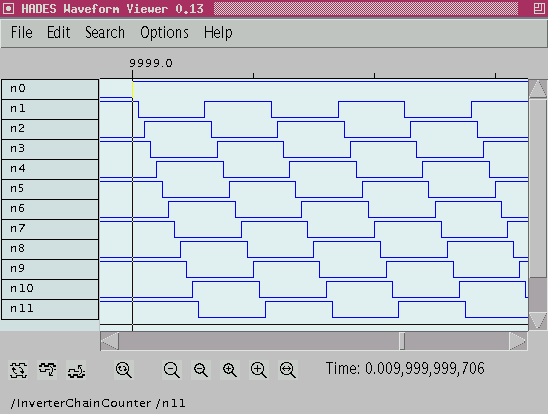 Ring oscillators are often used as prototype circuits
to test new semiconductor processes, because they are so simple
and therefore very easy to design.
They also allow to run the gates of the new process at optimal speed,
which is ideal to optimize the design parameters and layout rules
for the new process.
In such cases, usually one or a few of the gate outputs are
connected to buffers, which are then routed to output pads
of the integrated circuits and to external equipment like counters
and oscilloscopes.
While the single gates operate at very high frequencies
(e.g. a few picoseconds of delay), the resulting ring oscillator
output frequency is essentially divided by the number of gates in the
circuit and therefore accessible to external equipment.
Ring oscillators are often used as prototype circuits
to test new semiconductor processes, because they are so simple
and therefore very easy to design.
They also allow to run the gates of the new process at optimal speed,
which is ideal to optimize the design parameters and layout rules
for the new process.
In such cases, usually one or a few of the gate outputs are
connected to buffers, which are then routed to output pads
of the integrated circuits and to external equipment like counters
and oscilloscopes.
While the single gates operate at very high frequencies
(e.g. a few picoseconds of delay), the resulting ring oscillator
output frequency is essentially divided by the number of gates in the
circuit and therefore accessible to external equipment.