The image above shows a thumbnail of the interactive Java applet embedded into this page. Unfortunately, your browser is not Java-aware or Java is disabled in the browser preferences. To start the applet, please enable Java and reload this page. (You might have to restart the browser.)

Circuit Description

This applet demonstrates the famous Sieve of Eratosthenes algorithm on the TinyMips microprocessor. The hardware structure shown here consists of the processor, some glue logic, and a single RAM component that stores both the program and the data generated during program execution.

The Sieve of Eratosthenes algorithm

The C source code of the Sieve algorithm is shown below. The 'limit' variable defines the size of the sieve matrix, whose starting position is given by the hardcoded value of the 'sieve' pointer variable. In the example below the values 'limit=256' and 'sieve=0x00000200' were chosen, so that the sieve matrix starts near the end of the program code, and it is possible to watch instruction fetch accesses and sieve write accesses in the memory editor at the same time.

The program consists of four subsequent stages. The first stage initializes the sieve matrix in the address range sieve..sieve+limit with a constant value 0xcccccccc. This value is more or less arbitrary, and was chosen because it is visually quite different from small integer values like 0x00000007 and therefore easy to spot in the memory editor. In order to visualize the algorithm better, a full 32-bit memory word is used (or rather, "wasted") for each prime number. An optimized variant of the algorithm would only use a single bit of memory per prime-number, which makes for a nice bit-fiddling programming exercise. For details and references to much more elaborate prime-number algorithms, see D.E. Knuth, Art of Computer Programming.

Click here for a screenshot of the memory editor after the first few iterations of the loop. The next loop marks all multiples of two in the sieve array. The idea of the loop is to mark all numbers that are divisible by two as non-prime. (Note: the screenshots show an early version of the memory editor which still uses word-addresses: multiply by four to get the actual byte-addresses used in the software. The user-interface of the current memory editor shows byte-addresses.)

The third stage of the program consists of two nested loops and forms the heart of the sieve algorithm. The outer loop steps through all uneven numbers (3,5,7,..) up to the limit value. Naturally, we could also iterate through all numbers (2,3,4,5,6,...) but the previous loop has already marked all even numbers as non-prime. The inner loop marks all multiples of the currently active outer variable. Click here and here for screenshots of the memory editor after the first few iterations of the inner loop with values 3 and 5 as the outer loop variable. Once the outer loop finishes, all non-prime numbers inside the sieve array have been marked with their largest divisor, while the prime numbers still retain their initialization value 0xcccccccc.

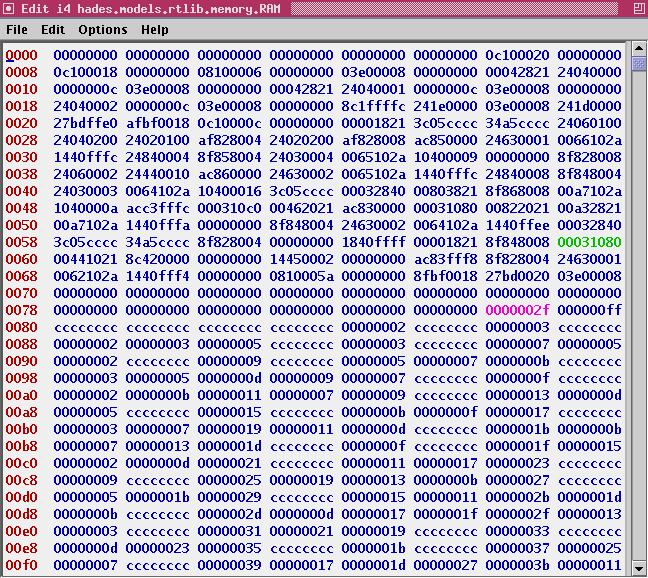
The final endless loop of the program steps through the sieve array. If the value in question still retains the marker value 0xcccccccc, the number is prime and its value is written to address sieve-2. The following screenshot shows the memory editor during execution of the final loop, with the value 0x2f (decimal 47) written to location sieve-2 as one of the calculated prime numbers. Make sure to check the values inside the sieve array starting at memory address 0x0200.

Usage

Wait until the applet is loaded. You can now open the memory-editor (via popup > edit) The memory editor highlights the last read operation in green color, and the last write operation in cyan color, which allows you to easily watch the program execution. The user-interface of the MipsRAM simulation component always shows the same byte-addresses as your software.

Again, the memory editor highlights the last read operation in green color, and the last write operation in cyan color, which allows you to easily watch the program execution. By default, the memory editor shows the more compact hexadecimal view of the memory contents, but you switch to the detailed disassembled view via its menu bar. To select either mode, open the format submenu from the editor's menu bar via menu>edit>format>hex, then select the corresponding view.

If you want to change the simulation speed, just select 'edit' on the clock-generator component, then edit the value of the clock-generator 'period' property, and select 'apply' (and 'ok' to close the clock-generator config dialog).

Similarly, open the TinyMips user-interface window (via popup > edit) to watch the register contents during the program execution.

The binary program running on the processor was compiled and linked with the GNU gcc (2.7.2.3) and binutils cross-compiler toolchain on a Linux x86 host, with the final ELF loading and relocation done via the Hades Elf2rom tool. See

• C source code
• disassembled ELF file
• memory-initialization file
• build-script/batch-file

• TinyMips sources (JAR archive)

/* sieve of Eratosthenes to demonstrate TinyMips in Hades */

static int limit;    // sieve size
static int *sieve;   // pointer to the sieve array


int main( int argc, char** argv ) {

  int i;
  int j;

  limit = 256; // 16384; 
  sieve = (void*) 0x00000200;

  // initialization loop
  for( i=0; i < limit; i++ ) {
    *(sieve+i) = 0xCCCCCCCC;
  }

  // first loop iteration marks all multiples of 2
  for( i=4; i < limit; i = i+2 ) {
    *(sieve+i) = 2;
  }

  // next nested loop marks all multiples of 3,5,7,...
  for( i=3; i < limit; i = i+2 ) {
    *(sieve-1) = i;

    for( j=(i+i); j < limit; j = j+i ) {
      *(sieve+j) = i;
    }
  }

  // endless loop that writes the detected primes to *(sieve-2)
  for( ;; ) {
    for( i=0; i < limit; i++ ) {
      if (*(sieve+i) == 0xCCCCCCCC) {
        *(sieve-2) = i;
      }
    }
  }
}