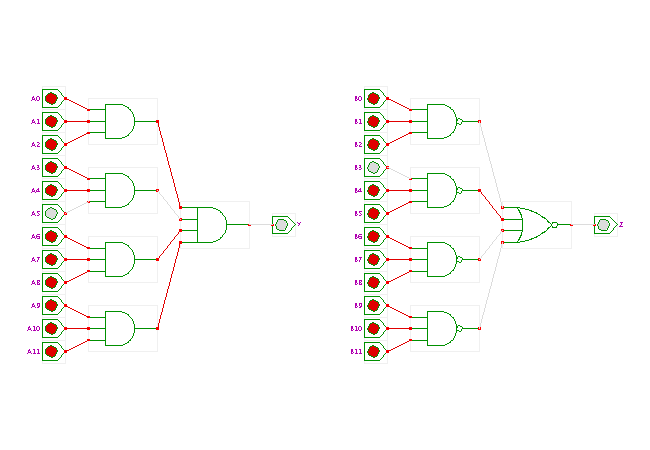| |
DescriptionTwo variants of a twelve-input AND gate.
As explained in the previous applets, technological reasons make it difficult or impossible to realize gates with more than about four inputs. Therefore, a circuit of multiple smaller gates is used to build gates with more than four inputs.
The circuit on the left part of the applet shows the trivial realization of the twelve-input AND gate, namely a two-level tree of three- and four-input gates. Naturally, many similar variants of the same architecture are also possible (for example, three four-input gates in the first level and one three-input gate in the second level).
The circuit on the right part of the applet shows a different realization based on the de'Morgan transformation. Here, the AND-gate in the second level of the tree is replaced by an OR-gate with inverted output (that is, a 3-input NOR). The inverted inputs are easily available by replacing the first-level AND-gates with NAND-gates.
In CMOS technology, two transistors are required for an inverter, and six and eight transistors are required for each three- and four-input NAND and NOR gate. As the non-inverting gates are built from the inverting gate followed by an inverter, the circuit on the left would use 42 transistors (6+2 for each AND3 gate and 8+2 for the AND4 gate), while the circuit on the right requires 32 transistors (6 for each NAND3 gate and 8 for the NOR4 gate). The circuit on the right is also almost twice as fast.
To explore the circuit, just click the corresponding switches, or type the bindkeys (0,1,2,3,4,5,6,7,8,9,a,b) to control the rightmost gate. No bindkeys are used for the gate on the left.
Run the applet | Run the editor (via Webstart)