7.3.4 Kanonische Normalformen

Eine kanonische Normalform ist eine Form, in die jede Funktion eindeutig gebracht werden kann.

Wichtig sind folgende Normalformen:

Disjunktive Normalform (DNF)

Konjunktive Normalform (KNF)

Reed-Muller-Form (RMF)

Es ist üblich die DNF bzw. die KNF aus sog. Mintermen bzw. Maxtermen aufzubauen. Minterme wurden schon unter der Bezeichnung Einspunktfunktion definiert:

Def. m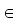Tn heißt Minterm , wenn es genau ein x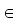Bn gibt, so dass m(x) = 1 und m(y) = 0 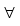y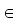Bn, y≠x .

M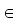Tn heißt Maxterm , wenn es genau ein x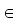Bn gibt, so dass M(x) = 0 und M(y) = 1 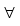y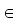Bn, y≠x .

In Tn gibt es genau 2n Minterme und 2n Maxterme.

Beispiel : T3 Tabellen für alle Minterme und Maxterme m1 ... m8 ; M1 ... M8

 a b c  |  m1 m2 m3 m4 m5 m6 m7 m8     M1 M2 M3 M4 M5 M6 M7 M8 
 _______|____________________________________________________ 
 0 0 0  |  1  0  0  0  0  0  0  0     0  1  1  1  1  1  1  1  
 0 0 1  |  0  1  0  0  0  0  0  0     1  0  1  1  1  1  1  1  
 0 1 0  |  0  0  1  0  0  0  0  0     1  1  0  1  1  1  1  1  
 0 1 1  |  0  0  0  1  0  0  0  0     1  1  1  0  1  1  1  1  
 1 0 0  |  0  0  0  0  1  0  0  0     1  1  1  1  0  1  1  1  
 1 0 1  |  0  0  0  0  0  1  0  0     1  1  1  1  1  0  1  1  
 1 1 0  |  0  0  0  0  0  0  1  0     1  1  1  1  1  1  0  1  
 1 1 1  |  0  0  0  0  0  0  0  1     1  1  1  1  1  1  1  0

Def. Sei f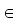Tn und fi seien die Elemente der Funktionstabelle von f (i = 1,...,2n) . Dann ist 

      2n                               
 f =  fi∩mi   =  f1∩m1  f2∩m2  f3∩m3  ...   
     i=1

die disjunktive Normalform (DNF) und 

      2n                               
 f = ∩ fiMi   =  (f1M1) ∩ (f2M2) ∩ (f3M3) ∩ ...     
     i=1

die konjunktive Normalform (KNF) von f .

Bei der Konjunktiven Normalform beachte man, dass aus fi = 1 folgt:
fimi = 1Mi = 1 . Diese Terme können also weggelassen werden.
Nur die Terme mit fi = 0 verbleiben in der konjunktiven Normalform.

Die Reed-Muller-Form (RMF) von f ist 

     2n                               
 f = Σ ri*pi    
     i=1

wo das Symbol Σ die wiederholte Addition im GF(2) bedeutet.
ri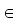B sind Koeffizienten und pi die rekursiv definierten Basisfunktionen

p1 = 1;
p2 = p1*x1 = x1
p3 = p1*x2 = x2
p4 = p2*x2 = x1*x2
p5 = p1*x3 = x3
p6 = p2*x3 = x1*x3
p7 = p3*x3 = x2*x3
p8 = p4*x3 = x1*x2*x3
p9 = p1*x4 = x4
usw.

Die xi sind die Variablen der Funktionen. Mit dem Infixsymbol * ist die Multiplikation im GF(2) also das UND gemeint.

Diese Basisfunktionen lassen sich automatisch erzeugen (hier mit den Variablen a, b, c, ...): 

rmbasis(1)


rmbasis(3)


rmbasis(5)