6.4 Vektorraum

Definition : A, B seien Mengen. Unter einer äußeren Verknüpfung von B mit A verstehen wir eine Abbildung f : A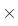B → B .

Definition : K sei ein Körper mit den inneren Verknüpfungen + und . Eine additive Abelsche Gruppe V mit der inneren Verknüpfung 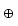und mit einer äußeren Verknüpfung KV → V , die jedem Paar (k,a) mit k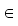K und a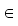V genau ein ka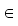V zuordnet, heißt ein linearer Raum oder Vektorraum über K , wenn die folgenden Axiome erfüllt sind:

 V1    k(ha) = (kh)a          k,h  K ,    a  V  
 V2    (k + h)a = ka  ha     k,h  K ,    a  V  
 V3    k(a  b) = ka  kb     k,h  K ,    a  V  
 V4    1a = a                     k,h  K ,    a  V  

Die Elemente von V heißen Vektoren , die von K Skalare . Die äußere Verknüpfung nennen wir linksseitige Multiplikation der Elemente von V mit den Elementen von K .

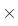Sehr wichtige Beispiele linearer Räume sind die n-fachen kartesischen Produkte KK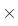 ... 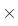K = Kⁿ eines Körpers K mit sich.
Die innere Verknüpfung von V wird in diesem Fall auf die Addition in K zurückgeführt:

Mit a = (a₁, a₂) und b = (b₁, b₂) , wo a₁, a₂, b₁, b₂ 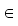K gilt

a b = (a₁ + b₁, a₂ + b₂)

Die äußere Verknüpfung ist entsprechend definiert:

ka = (ka₁, ka₂)

Der Nachweis, dass die Axiome des Vektorraumes mit diesen Festlegungen immer erfüllt sind, sei dem Leser als einfache Übung überlassen.

Die Körperelemente a₁, a₂, ... eines solchen Vektors a = (a₁, a₂, ... ) nennt man Komponenten .

Vektorräume sind so vielseitig einsetzbar, dass sie als eigene mathematische Disziplin die Lineare Algebra begründen. Wir werden nur weniges aus diesem Gebiet benötigen (z. B. die Matrizenmultiplikation), das sich aber kaum ohne Gesamtdarstellung verständlich sagen lässt. Wir verweisen deshalb auf die sehr umfangreiche Lehrbuchliteratur.

Für die Technische Informatik wichtig sind insbesondere die Kartesischen Produkte der Menge {0,1} . Ihre Elemente sind Vektoren aus je n Bits. Die innere Verknüpfung ist definiert wie oben erläutert und entspricht einem exklusiven Oder Komponentenweise. Für das exklusive Oder gibt es in MATLAB die Funktion xor in Präfixnotation. Äquivalent ist aber auch das Ungleich in Infixnotation (~=). Die Multiplikation im GF(2) entspricht dem logischen Und (&). Damit ist die lineare Algebra über dem GF(2) sehr einfach in MATLAB realisierbar:

a = [0 1 1 1 0 1 0 0];       % ein Vektor
b = [0 0 0 1 1 1 1 0];       % ein zweiter Vektor
c = a ~= b;  result2fig(c);  % Vektoraddition
d = 0 & a;   result2fig(d);  % äußere Verknüpfung mit 0
f = 1 & a;   result2fig(f);  % äußere Verknüpfung mit 1

Entsprechendes tut die Funktion demovectorop(a,b) , mit einem Skalar und einem Vektor bzw. zwei Vektoren als Parameter:

demovectorop([1 0 1 1],[0 1 1 0])

demovectorop(0,[0 1 1 0])

demovectorop([1 0 1 1],1)

Lineare Transformationen lassen sich mit Matrizen sehr einfach formulieren und realisieren. Ein Beispiel gibt die folgende Graphik, in der ein durch fünf Eckpunkte definiertes zweidimensionales Objekt dadurch gedreht wird, dass die Matrix der fünf Punkte mit der 2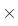2-Drehmatrix A vormultipliziert wird:

p  = [ -0.5  +0.5  -0.5  +0.5  0;  0  0  1  1  1.5 ];  % Eckpunkte der Graphik
j  = [1 2 4 5 3 4 1 3 2];                              % Reihenfolge der Punkte
w  = 70/180*pi;                                        % Drehwinkel 70°
A  = [cos(w)  -sin(w);  sin(w)  cos(w)];               % Transformationsmatrix
q  = A*p;                                              % gedrehte Punkte       
fh = fullscreen('Drehung');                            % Graphikfenster
patch(p(1,j),p(2,j),'g')                               % Objekt ungedreht, grün
patch(q(1,j),q(2,j),'r')                               % Objekt gedreht, rot
axis([-2 +2 -1.5 +1.5]);  axis off                     % Skalierung

Diese Codesequenz ist Kern folgender Funktion:

demotransformation

Parameter sind die Eckpunktmatrix, der die Reihenfolge der Punkte festlegende Indexvektor j und der Drehwinkel. Eine zufällige Graphik und ihre Drehung um 180 Grad liefert:

demotransformation( rand(2,5), 1:5, 180 )

Ist der erste Parameter eine 3*n-Matrix, so wird eine 3D-Graphik erstellt, die mit der Maus drehbar ist. Die Drehung um den Winkel w erfolgt um die z-Achse:

demotransformation( rand(3,10), [1:10, randpermut(10)], 180 )

Lösung von linearen Gleichungssystemen im GF(2) :

A = [1 1 0; 1 1 1; 0 1 1]

r = randb(3)';          % rechte Seite des Gleichungssystems

x = bingausselim(A,r)   % Lösung des Gleichungssystems  A*x = r

mod(A*x+r,2)            % Prüfung der Lösung

bingausselim( [1 1 0; 1 1 1; 0 1 1] , [0 1 1]' )