
 |  |
 Description
This applet demonstrates a floating-point multiplier.
The number representation is based on the same principles as the
single-precision and double-precision formats defined by the
the IEEE 754 standard.
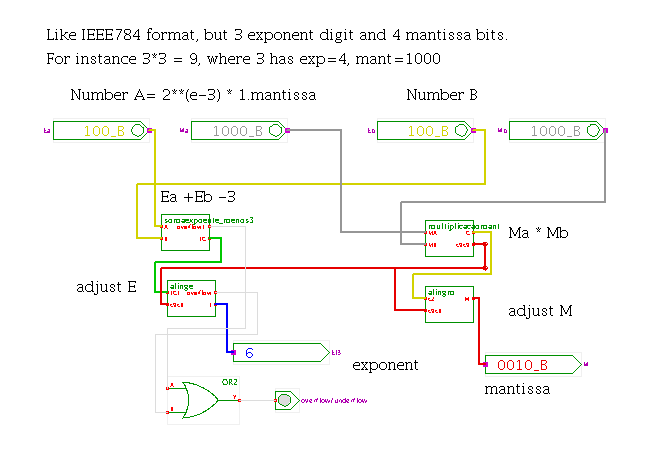
However, the multiplier shown here only uses a four-bit normalized
mantissa and a three-bit exponent (with offset 3), without sign-bits.
That is, a number is represented as
Description
This applet demonstrates a floating-point multiplier.
The number representation is based on the same principles as the
single-precision and double-precision formats defined by the
the IEEE 754 standard.
However, the multiplier shown here only uses a four-bit normalized
mantissa and a three-bit exponent (with offset 3), without sign-bits.
That is, a number is represented as
value = 2(exponent-3) * (1.0 + mantissa * 2-4)
For details and a few examples, please read the short introduction to the floating-point representation. The following table summarizes the number of bits used here and in the single- and double-precision standard representations:
number of bits total sign exponent (offset) mantissa ---------------------------+------------------------------------------ this applet 7 0 3 3 4 IEEE-754 single-precision 32 1 8 127 23 IEEE-754 double-precision 64 1 11 1023 52
Click or shift+click the input switches to increment or decrement the input values for the A and B exponents and mantissae, and watch the resulting output value. For example, the initial values for both numbers are exponent=100b and mantissa=1000b, which corresponds to a value of
A = B = 2(4-3)*(1.0 + 8/16) = 2*1.5 = 3
Not surprisingly, the resulting multiplier output is exp=110b and mantissa=0010b, or
R = 2(6-3)*(1.0 + 2/16) = 8*1.125 = 9
You can open new editor windows for all subcomponents (popup-menu, select 'edit') to study the actual gate-level implmentation of the multiplier. A real floating-point multiplier just uses a much larger array (e.g. 23*23 for single-precision and 52*52 for double-precision), but the princile stays the same. Also, note that the muliplication of signed-numbers poses no problem; the sign bit is just the XOR or the two operand sign bits.
Run the applet | Run the editor (via Webstart)