Aufgaben zur Vorlesung Technische Informatik 1


	Informatik / TAMS / Applets / Jython Console / T1: Einschrittige Codes

Beschreibung	Diese Seite demonstriert die Überprüfung von Übungsaufgaben über speziell dazu vorbereitete Funktionen. Das gewählte Beispiel, einschrittige Codes, ist auch dadurch interessant, dass die Aufgabe mehrere (sehr viele) gleichwertige korrekte Lösungen aufweist. Ein einfacher Vergleich der von den Studierenden ermittelten Lösung mit einer eindeutigen Musterlösung scheidet dadurch aus; der Vergleich mit einer vorberechneten Menge von korrekten Lösungen scheitert an der enormen Anzahl der möglichen Lösungen. Die Applets auf dieser Seite verwenden wieder die digital-signierte Version unserer interaktiven Jython-Console und laden bei Bedarf kleinere Jython-Skripte direkt vom Webserver nach. Abhängig von den Sicherheitseinstellungen Ihres Browsers bzw. ihres JREs bekommen Sie eventuell eine Nachfrage und Warnung. Bitte bestätigen Sie die Ausführung des signierten Applets.
Einschrittige Codes	Erzeugung einschrittiger Codes Das folgende Applet generiert einen einschrittigen Code mit der als Parameter übergebenen Anzahl von Codewörtern. Bei gerader Anzahl von Codewörtern ist der Code zyklisch-einschrittig. Um den Aufbau des Codes deutlicher zu zeigen, werden die einzelnen Codewörtern als Binärzahlen ausgegeben: Die vom Applet benutzte Funktion `einschritt()` zur Konstruktion eines einschrittigen Codes mit n Codewörtern basiert übrigens auf einer ganz einfachen Idee: Angenommen, man besitzt bereits einen einschrittigen Code mit n/2 Codewörtern. Dann erhält man die erste Hälfte eines Codes mit n Wörtern durch Erweitern der vorhandenen Codewörter um eine führende 0. Die zweite Hälfte erhält man durch Erweitern der vorhandenen Codewörter um eine führende 1 und Umkehren der Reihenfolge. Die Basis zur Konstruktion sind die beiden Codes (0) und (0,1) mit ein bzw. zwei Codewörtern.
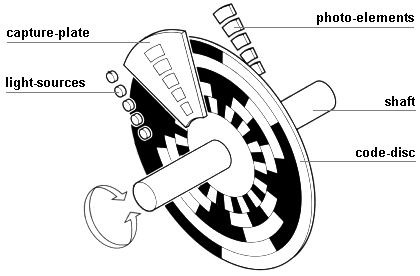
Anwendung und Eigenschaften einschrittiger Codes	Vergleich einschrittiger und nicht-einschrittiger Codes. Eine wichtige Anwendung einschrittiger Codes ist die Konstruktion von zuverlässigen Positionsgebern. Die folgende Abbildung zeigt das Aufbauprinzip eines Drehgebers mit 5 bit Auflösung, also etwa 10 Grad Winkelauflösung: Offenbar kann es zu Ablesefehlern kommen, wenn ein Hell/Dunkel-Wechsel genau auf Höhe eines Sensorelements liegt. Der zentrale Unterschied zwischen einschrittigem und normalem Binärcode wird im folgenden Applet demonstriert. Das nachfolgende Applet erzeugt einen einschrittigen Code der angegebenen Länge. Anschließend werden die Codewörter in ihre einzelnen Bits zerlegt und mit einen schwachen Jitter überlagert, d.h. zeitlich leicht gegeneinander versetzt (oberer Plot). Der untere Plot zeigt die Dekodierung dieses verrauschten Signals als Binärzahlen. Zum Vergleich wird die gleiche Darstellung auch mit einem gewöhnlichen Binärcode erzeugt. Bei einschrittigen Codes ist der Ablesefehler also maximal ein Bit, bei nicht einschrittigen Codes dagegen (n/2).
Überprüfung	Automatische Überprüfung, komplexe Aufgabenstellung mit vielen möglichen und gleichwertigen Lösungen. Aufgabe T1_2_5: Finden Sie einen zyklisch-einschrittigen Binärcode mit 12 Codewörtern! Ein solcher Code könnte zum Beispiel zur Winkelcodierung in 30-Grad-Schritten benutzt werden. (Die voreingestellte Inhalt in diesem Applet enthält bereits eine korrekte Lösung. Bitte versuchen Sie, eine weitere korrekte Variante zu finden!). Die folgende Graphik veranschaulicht drei typische Lösungen der Aufgabe in einem KV-Diagramm:
	Automatische Überprüfung Ein Beispiel für eine noch nicht korrekte Lösung. Bitte den Überprüfen-Knopf drücken, um die zugehörige Hilfestellung anzuzeigen: Ein weiteres Beispiel für eine noch nicht korrekte Lösung. Bitte den Überprüfen-Knopf drücken, um die zugehörige Hilfestellung anzuzeigen: Ein weiteres Beispiel für eine noch nicht korrekte Lösung. Bitte den Überprüfen-Knopf drücken, um die zugehörige Hilfestellung anzuzeigen: Noch ein Beispiel für eine noch nicht korrekte Lösung. Bitte den Überprüfen-Knopf drücken, um die zugehörige Hilfestellung anzuzeigen:
14.07.2004 Impressum	http://tams-www.informatik.uni-hamburg.de/applets/jython/index.html