Beim Entwurf von Schaltnetzen geht man aus von einer eindeutigen Verhaltensbeschreibung durch binäralgebraische Ausdrücke, Funktionstabellen oder BDDs etc.. Entwurfsfreiheiten bestehen in der Wahl der realisierenden Struktur. Dieses gilt also für den Entwurf der δ- und λ-Schaltnetze von Schaltwerken auch. Der grundsätzliche Unterschied beim Entwurf eines Schaltwerkes besteht jedoch darin, dass die Zustandsvariablen zi Eingangsgrössen der beiden Schaltnetze sind. Sowohl die Anzahl dieser binären Zustandsvariablen wie auch die Codierung der Zustände in diesen Variablen zi gehören zu den Freiheiten des Entwurfs eines Schaltwerkes. Selbst die Zahl der benötigten Zustände liegt nicht fest.
Ziel beim Entwurf eines Schaltwerkes ist wie beim Schaltnetz eine Realisierung mit geringem Aufwand. Neben den beiden Schaltnetzen sind auch die Zeitglieder zu realisieren. Wir nehmen in diesem Abschnitt deren Realisierung als rückflankengesteuerte Flipflops an. Die Zahl der Zustandsvariablen und vor allem die Codierung der Zustände hat erheblichen Einfluss auf die beiden Schaltnetze. Die Zusammenhänge sind so komplex, dass es kein Verfahren zur Minimierung des Realisierungsaufwandes gibt, welches alle Entwurfsfreiheiten benutzt. Die Verfahren bieten also alle nicht die Garantie, dass eine gefundene Lösung nicht zu verbessern ist.
Der Entwurf getakteter Schaltwerke erfolgt meistens in sechs Phasen:
1. Spezifikation textuell oder grafisch z.B. mit dem Zustandsdiagramm
2. Aufstellen der formalen Übergangstabelle
3. Reduktion der Zahl der Zustände
4. Wahl der Zustandscodierung und Aufstellen der Übergangstabelle
5. Minimierung der Schaltnetze
6. Überprüfung des realisierten Schaltwerks
Bei Unzufriedenheit mit dem Ergebnis geht man zurück nach 4., evtl. auch nach 2. letzteres evt. ohne 3.
Die Entwurfsphasen sollen nachfolgend an einem Beispiel erläutert werden:
(1) Ausgangspunkt sei folgendes Zustandsdiagramm:
drawfsm( [1 2; 3 4; 1 4; 5 6; 1 6; 7 6; 1 6] )
(2) Aus dem Zustandsdiagramm folgt die Übergangstabelle, die hier wieder in Form der Flusstafel dargestellt wird. Wir fügen noch eine Ausgabetafel für das Mealy-Modell an:
fsmtab(...
{ [1 2; 3 4; 1 4; 5 6; 1 6; 7 6; 1 6];... % Übergangstabelle
1 + [0 0; 0 0; 0 0; 0 1; 0 1; 0 1; 0 1]},...
{'A';'B';'C';'D';'E';'F';'G'},...
1,...
0,...
{'00';'01';'11';'10'},...
'',...
{'0';'1'}...
)
(3) Meistens weist ein Zustandsdiagramm bei der Spezifikation mehr Zustände auf als nötig. Wenn nämlich zwei Zustände für alle möglichen Eingaben jeweils die selben Folgezustände und auch die selben Ausgaben haben, so kann man diese äquivalenten Zustände als den selben betrachten.
Definition: Zwei Zustände zi und zj heissen äquivalent, wenn
λ(zi) = λ(zj) beim Moore-Schaltwerk bzw.
λ(x,zi) = λ(x,zj) 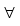 x beim Mealy-Schaltwerk
x beim Mealy-Schaltwerk
und entweder
δ(x,zi) = δ(x,zj)
oder
δ(x,zi) äquivalent δ(x,zj) 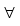 x .
x .
Die Äquivalenz ist offensichtlich einfach automatisch zu prüfen. Bei der Elimination
eines der beiden äquivalenten Zustände müssen Referenzen auf ihn durch Referenzen
auf den äquivalenten ersetzt werden. Dies tut die Funktion elimeqs .
Damit ergeben sich das folgende reduzierte Zustandsdiagramm und die reduzierte
Flusstafel:
result2fig(...
select(...
elimeqs(...
{[1 2; 3 4; 1 4; 5 6; 1 6; 7 6; 1 6];...
1 + [0 0; 0 0; 0 0; 0 1; 0 1; 0 1; 0 1]}...
),...
1)...
);
result2fig(...
select(...
elimeqs(...
{[1 2; 3 4; 1 4; 5 6; 1 6; 7 6; 1 6];...
1 + [0 0; 0 0; 0 0; 0 1; 0 1; 0 1; 0 1]}...
),...
2)...
);
Das Schaltwerk ist in der Funktion gleich geblieben:
:
demofsm( ...
select( ...
elimeqs( ...
{[1 2; 3 4; 1 4; 5 6; 1 6; 7 6; 1 6]; ...
1 + [0 0; 0 0; 0 0; 0 1; 0 1; 0 1; 0 1] }...
)...
,1)...
)
Die Äquivalenz der beiden Zustände E und G war unmittelbar in der ursprünglichen Flusstafel zu erkennen. Dass auch D und F äquivalent sind, ergibt sich erst als Folge der Äquivalenz von E und G .
(4) Die Wahl einer binären Codierung der Zustände ist bei getakteten Schaltwerken in keiner Weise eingeschränkt. Bisweilen ist der Realisierungsaufwand sogar am kleinsten, wenn der Block-Code mehr Bits enthält als erforderlich. Im vorliegenden Fall benötigen wir wenigstens 3 Zustandsbits, um die 5 Zustände zu codieren. Das sind nicht weniger Bits als zur Codierung der 7 Zustände des ursprünglichen Zustandsdiagramms erforderlich gewesen wären. Dennoch lohnt sich die Reduktion des Zustandsdiagramms, da die nicht belegten Zustände als nicht spezifizierte Punkte (Do'ntCares) in den KV-Diagrammen der δ- und λ-Schaltnetze auftauchen und so zur Vereinfachung nützlich sind. In unserem einfachen Fall wollen wir die Zustände mit 3 Bits codieren. Die Anzahl der möglichen Zustandscodierungen von n Zuständen mit k Bits ist gleich der Zahl der Variationen der 2k Binärwörter zu je n Zuständen, nämlich
fsmcod
In dieser Tabelle wurde jeweils die minimale Anzahl k von Zustandsbits für die gegebene Anzahl n von Zuständen gewählt. In unserem Fall sind es 6720 Möglichkeiten. Die wollen wir nicht alle untersuchen sondern nur zwei:
(a) Die Zustände A,B,C,D,E werden binär codiert der Reihe nach durch 000 001 010 011 100 .
(b) Die Codierung wird generiert nach folgendem Verfahren:
Man färbe alle Kanten des Zustandsdiagramms jeweils mit dem Hammingabstand der Codierungen der Knoten, die die Kante verbindet, und versuche die Summe aller Farben durch geeignete Codierung zu minimieren.
Diese Heuristik ist plausibel, denn sie bewirkt, dass sich bei Änderung von x oder eines der Zustandsbits meist nur ein Ausgang ändert, während die anderen konstant bleiben. Die Einsen im KV-Diagramm des δ-Schaltnetzes liegen also meist zusammen, so dass grosse Schleifen möglich sind.
Die Zustandsdiagramme für beide Codierungen sind:
drawfsmcod
(5) Aus diesen Diagrammen entnimmt man die Funktionstabellen der drei binären Funktionen des δ-Schaltnetzes. Hinzu kommt in diesem Fall nur eine Schaltfunktion für die Ausgabe. Die Funktionswerte kann man in KV-Diagramme eintragen und anschliessend eine Bündelminimierung vornehmen.
minfsmcoda
Die Minimierung ergibt:
h = z1∩x
z1next = z2∩z3∩x'
z2next = z2∩x  z2'∩z3
z2'∩z3  h
z3next = x
y = h
h
z3next = x
y = h  z2∩z3∩x
z2∩z3∩x
Die Aufwandsmasse sind hierfür M1 = 7 und M2 = 17
Für die Zustandscodierung (b) haben wir:
minfsmcodb
Die Minimierung ergibt:
y = z1∩x
z1next = z1∩z3  z3∩x
z3∩x  y
z2next = z1'∩z2'∩z3∩x
z3next = z2next
y
z2next = z1'∩z2'∩z3∩x
z3next = z2next  x
x
Die Aufwandsmasse sind hierfür M1 = 6 und M2 = 15 . Der Aufwand ist bei der Codierung (b) bezüglich beider Aufwandsmasse etwas geringer als bei Codierung (a). Man wird also die Zustandscodierung (b) benutzen.
(6) Das entworfene Schaltwerk entspricht der Spezifikation. Eine abschliessende Überprüfung ist dennoch sinnvoll, weil die Spezifikation häufig Randbedingungen nicht ausdrücklich nennt, die aber eingehalten werden müssen. Z.B. könnte es sein, dass das Schaltwerk beim Einschalten in einen in der Spezifikation nicht vorkommenden Zustand gerät, der nur Schlingen aufweist und damit keinen Weg zum vorgesehenen Schaltwerk hat. Wenn die Spezifikation nicht eine Eingabe vorsieht, die das Schaltwerk in einen definierten Grundzustand bringt (sog. Reset) und wenn eine Zustandscodierung gewählt wurde, die mehr Zustände ermöglicht als benötigt, dann ist dieser sechste Schritt wichtig.
Wir müssen also das Zustandsdiagramm mit allen 2k Zuständen untersuchen, das durch die ermittelten schaltalgebraischen Ausdrücke realisiert wird. Wir notieren also zunächst die schaltalgebraischen Ausdrücke für die drei Zustandsbits. Daraus wird für sämtliche 8 möglichen Zustände mal 2 Inputs der Folgezustand berechnet, um die Übergangstafel zu ermitteln. Nach dieser wird das Zustandsdiagramm gezeichnet. Wir automatisieren dies für beide Zustandscodierungen.
Zustandscodierung (a)
demofsmcoda
Zustandscodierung (b)
demofsmcodb
Offenbar führen in beiden Fällen zufälligerweise alle Kanten von den zusätzlichen Knoten direkt zum gewünschten Automaten. Wenn man nach dem Einschalten einen Takt gibt, so wird sich dieses Schaltwerk mit Sicherheit in einem der vorgesehenen Zustände befinden. Dass zusätzliche Zustände völlig isoliert sind, ist zwar selten, aber es kommt vor. Abhilfe ist dann relativ einfach. Unter Beibehaltung der Zustandscodierung kann man im KV-Diagramm einen oder mehrere Do'ntCares gezielt je nach Erfordernis auf 0 oder 1 setzen und das Schaltnetz neu minimieren.
Damit ist der Entwurf des Schaltwerkes abgeschlossen.