Zahlen wurden in der frühen menschlichen Geschichte zunächst mithilfe von Zählsymbolen dargestellt. Bei Bargeld ist dies bis heute üblich. Die Addition wird einfach durch das Zusammenwerfen realisiert. Wenn die Summe zu unhandlich ist, kann irgendwann durch einfaches Ersetzen (bei Geld das sog. Wechseln) einer festgelegten Anzahl niederwertiger Zählsymbole durch ein Zählsymbol höheren Wertes eine handlichere Repräsentation erreicht werden.
Um das Jahr -2000 herum, heute also vor etwa 4000 Jahren, wurde die Stellenorientierte Zahlendarstellung in Babylon erfunden. Die Basis der Darstellung war nicht wie heute üblich 10 , sondern 60 . Man nennt es das Sexagesimalsystem. Es hat sich in der Zeit- und der Winkeleinteilung erhalten. Die Notation der 60 Ziffern erfolgt durch die schon vor der Erfindung des Systems benutzten Zählsymbole für Einer und Zehner. Wir benutzen hier anstelle der platzsparenden Stifteindrücke im Ton die Symbole 1 und < . Die Benutzung von Zählsymbolen hat die Folge, dass die Ziffer 0 kein Zählsymbol erhält, also nicht geschrieben wird. Tatsächlich haben die Babylonier nur selten Fehler gemacht, obwohl die Schreibweise mehrdeutig war. Ein Beispiel für solch einen Fehler wird gleich behandelt werden.
Die Darstellung nicht negativer ganzer Zahlen x beruht auf deren eindeutiger Zerlegung nach
n-1
x = Σ zi bi
i=0
wo für alle sog. Ziffern gilt: 0 ≤ zi < b .
Im Dezimalsystem mit b = 10 bedeutet die Schreibweise 743 die Zahl mit dem Wert
x = 7*102 + 4*101 + 3*100 .
Entsprechend bedeutete die Schreibweise <11 <<111 in Babylon die Zahl mit dem Wert
x = 12*601 + 23*600 = 743 .
Es könnte aber auch z.B. 12*602 + 23*600 gemeint sein, weil 0*601 nicht notiert wurde. Ein Beispiel für solch einen (seltenen) Fehler zeigt eine altbabylonische Schultafel, auf der die Potenzen von 100 im Sexagesimalsystem bis 10010 berechnet werden:
Wie haben wir es doch einfach: Die Funktion powersbabylon(z,n) schafft dies in einem Augenblick:
Die Ziffer 0 ist hier im Gegensatz zur babylonischen Schreibweise zu erkennen an der größeren Lücke in der Zeile 6. Unserem Mathematiker aus Babylon wollen wir zugute halten, (1) dass die Zahlen, mit denen er hantierte z.T. deutlich größer sind als die Anzahl der Sekunden, die seit dem Urknall bis heute abgelaufen sind und (2) dass auf der Rückseite der Tafel eine entsprechende Tabelle der Potenzen von 5 fehlerfrei ausgerechnet ist. Wir können das hier nachrechnen:
Obige MATLAB-Zeile selektieren, dann "c" tippen. Es erscheint der MATLAB-Block im
Editor. Dort für zahl in babylonisch anstelle der '1 <<<<' die zu potenzierende Zahl
einsetzen, z.B. '11' oder '11111' für 2 bzw. 5 , und dann unter Tools 'run' klicken.
Das selbe kann man natürlich auch ins Matlab-Kommandofenster eingeben.
Wer Matlab nicht installiert hat, kann t1runner verwenden.
Für den Interessierten gibt es hier zwei Funktionen zur (linearen textuellen) Darstellung der babylonischen Schreibweise von Zahlen und ihrer Rückwandlung sowie für die Addition und Multiplikation beliebig großer Zahlen:
Bei dieser Gelegenheit können Sie auch die Tabelle der Potenzen von 100 z.B. bis n = 16 ausgeben lassen und nachrechnen, ob es stimmt.
Auch wenn heute das Sexagesimalsystem schwerfällig erscheint, so war es für die damaligen Verhältnisse recht gut geeignet. Insbesondere die in einer durch und durch verwalteten Gesellschaft wichtige Operation der Teilung durch 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 ist in diesem System zu realisieren durch eine einfache Multiplikation mit 30, 20, 15, 12, 10, 6, 5, 4, 3, 2 und eine Stellenverschiebung. Nur wenig aufwendiger ist die Division durch 8 und 9 . Vermutlich war genau dies der Grund für die Einführung des Systems. Dann muss man die Erfindung als genial bezeichnen, denn es gibt kein besseres System, in dem Arithmetik mithilfe handhabbarer Tabellen so gut durchgeführt werden konnte.
Die Repräsentation von nicht negativen ganzen Zahlen und Brüchen in Stellensystemen zur Basis b wird im folgenden mit interaktiven Graphiken erläutert.
Die MATLAB-Funktion stellen2stellen(q,z) stellt den Algorithmus zur
Umrechnung zwischen Stellensystemen dar. Die Parameter bedeuten:
q : Basis des Stellensystems
z : darzustellende Zahl
q und z können interaktiv geändert werden. Eingaben immer mit der Eingabetaste abschließen ! Der Algorithmus wird durch Klicken in das grüne Taktfeld schrittweise ausgeführt.
Dieser Algorithmus führt direkt zur Funktion demostellen , die die Umrechnung in Matlab durchführt:
function stellen = demostellen(basis,zahl)
a = zahl;
i = 1;
while a > 0
stellen(i) = mod(a,basis);
a = div(a,basis);
i = i + 1;
end
Das Ergebnis liegt hier in Form eines Vektors von Stellen vor beginnend mit der niederwertigsten Stelle. Um in den folgenden Beispielen die übliche Darstellung beginnend mit der höchstwertigen Stelle zu erhalten, kehren wir den Vektor mit reverse um :
Die Umwandlung echter Brüche in die Stellendarstellung erfolgt mit einem geringfügig geänderten Algorithmus. Die Numerierung der Stellen erfolgt dabei vom Komma ausgehend nach rechts:
function stellen = demoechtbruch(basis,zahl,n)
a = zahl*basis;
for i=1:n
stellen(i) = floor(a);
a = (a - floor(a))*basis;
end
Beispiele:
Durch Kombination beider Verfahren können beliebige Zahlen umgewandelt werden. Dazu wird die Zahl aufgeteilt in den ganzzahligen Teil und einen echten Bruch:
function stellen = demobruch(basis,zahl,n) % Stellen-orientierte Zahlendarstellung zur Basis basis. % basis : Basis der Darstellung (natürliche Zahl>1) % zahl : darzustellende Zahl % n : Anzahl der gewünschten Nachkommastellen
a = floor(zahl);
b = zahl - a;
i = 1;
while a > 0
vstellen(i) = mod(a,basis);
a = div(a,basis);
i = i + 1;
end
a = b*basis;
for i=1:n
nstellen(i) = floor(a);
a = (a - floor(a))*basis;
end
stellen = [num2basstr2(reverse(vstellen)',basis)' '.' num2basstr2(nstellen',basis)'];
Die letzte Zeile des Programms wandelt die Vektoren der Vorkommastellen und der Nachkommastellen in einen Ausgabestring um.
Beispiele:
Arithmetik
Realisierung der Arithmetik
(a) Addierer
Gegeben seien zwei Zahlen in Stellendarstellung zur Basis b :
n-1 n-1
x = Σ xi bi ; y = Σ yi bi
i=0 i=0
Ihre Summe ist
n-1 n-1 n-1
x + y = Σ xi bi + Σ yi bi = Σ (xi + yi) bi
i=0 i=0 i=0
Wegen 0 ≤ xi < b und 0 ≤ yi < b gilt 0 ≤ (xi + yi) ≤ 2(b - 1) . xi + yi kann damit größer als b - 1 sein, es ist sind also nicht eine Ziffern des Resultats. Um die Ziffern des Resultats zu ermitteln, ist obiger Ausdruck für die Summe in den Algorithmus zur Berechnung der Stellendarstellung (siehe demostellen ) einzusetzen. Man erhält folgenden Algorithmus für die Addition:
c0 = 0
for i = 0 to n-1
zi = (xi + yi + ci) mod b
ci+1 = (ci + xi + yi) div b
end
Die ci nennt man Überträge. Eine Hardware, die aus den zwei gegebenen Stellen der Operanden xi und yi sowie dem Übertrag ci die Stelle zi der Summe und den Übertrag in die nächste Stelle ci+1 berechnet, nennt man Volladdierer. Eine Simulation in MATLAB liefert die Funktion fulladd :
function [s,c] = fulladd(a,b,ci,q) % [s,c] = fulladd(a,b,ci,q) % Volladdierer für Stellensysteme zur Basis q
if nargin<4 q = 2; end;
z = a + b + ci;
s = rem(z,q);
c = floor(z/q);openbyextension('fulladd.m')
Mit dem Volladdierer lässt sich ein serieller Addierer für Stellensysteme zur Basis q sehr einfach realisieren wie hier in der Funktion add :
function [s,co] = add(a,b,ci,q)
c = ci;
for k=1:length(a)
[s(k),c] = fulladd(a(k),b(k),c,q);
end
co = c;
Die Vektoren mit den Stellen der Summanden und des Resultats sind hier beginnend mit der niederwertigsten Stelle numeriert. Für die übliche Darstellung muss man sie mit der Funktion reverse umkehren:
Ein Addierer für beliebig große ganze Zahlen zur Basis q , die als Strings vorliegen, ist in der Funktion stradd realisiert. Negative Zahlen werden durch ein voranstehendes "-" gekennzeichnet. Für effizientes Rechnen ist diese Funktion natürlich nicht geeignet.
Beispiele:
Innerhalb von Matlab wird die Arithmetik mit 52 Bit durchgeführt. Die interne Arithmetik liefert deshalb ungenaue Ergebnisse, wenn zur Darstellung der Zahlen mehr als 52 Bits erforderlich sind. Die Funktion teststradd( q , n ) erzeugt zwei zufällige Operanden mit n Stellen zur Basis q . Ausgegeben werden die Operanden, das Resultat und die Differenz zwischen dem Resultat und dem Ergebnis der Rechner-internen Arithmetik.
Bis zu 15 Dezimalstellen ist die Rechner-interne Arithmetik genau:
Bei größeren Zahlen kann das Ergebnis ungenau werden:
Der zu stradd äquivalente Multiplizierer ist strmult :
Beispiele:
Auch hier gigbt es die zu teststradd äquivalente Funktion teststrmult :
Als weiters Beispiel liefert die Funktion strpowers(z,n) eine Liste sämtlicher Potenzen von z bis n :
Repräsentation negativer Zahlen durch Komplemente
Durch Hinzufügung eines Vorzeichenbits zu der oben betrachteten Stellenorientierten Darstellung könnte man negative und positive Zahlen repräsentieren. Bei der üblichen Dezimalschreibweise wird das faktisch so gemacht. Anstelle der Symbole 0 und 1 für das Vorzeichenbit werden dabei die Symbole + und - benutzt. Der Leser wird sich noch daran erinnern, wie er in der Grundschule den im Vergleich zum Addieren komplizierteren Algorithmus zum Stellen-orientierten Subtrahieren lernte. Dieses Subtrahieren, und damit die dazu benötigte Hardware im Rechner, wird überflüssig, wenn negative Zahlen als Komplemente repräsentiert werden, die nicht negativ sind.
Seien b die Basis der Darstellung sowie n die Anzahl der Vorkommastellen und m die Anzahl der Nachkommastellen. Dann definiert man für eine gegebene Zahl z < bn zwei Komplemente:
Die Funktion complements( z , b , n , m ) berechnet folgendes:
Kb = bn - z % das b-Komplement
Kb1 = bn - b-m - z % das (b-1)-Komplement
DKb = num2basstr2(Kb,b,n,m) % das b-Komplement in Darstellung zur Basis b
DKb1 = num2basstr2(Kb1,b,n,m) % das (b-1)-Komplement in Darstellung zur Basis b
Beispiele;
Berechnen Sie zur Übung die Komplemente für folgende Fälle:
| b | n | m | z |
|---|---|---|---|
| 10 | 2 | 3 | (2.475)10 |
| 2 | 4 | 2 | (10.01)2 |
Wichtig ist die Eigenschaft, dass das Komplement des Komplements die Identität ist:
Kb(n)(Kb(n)(x) = bn - Kb(n)(x) = bn - (bn - x) = x
Die Komplemente können im Stellensystem zur Basis b auf einfache Weise ohne Subtraktion direkt berechnet werden. Mit den Darstellungen
bn = (100...0)b ( n Nullen nach der 1 )
b-m = (0.00...01)b ( m-1 Nullen zwischen . und 1 )
ergibt sich
bn - b-m = αα...α.α...αα mit α = b - 1
(n Ziffern α vor dem Punkt und m Ziffern α nach dem Punkt)
Also
n
bn - b-m = Σ α bi
i=-m
Damit ist die Stellendarstellung des (b-1)-Komplements von
n
z = Σ zi bi
i=-m
gegeben durch
n
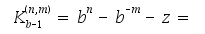 Σ (α - zi) bi
i=-m
Σ (α - zi) bi
i=-m
Die Differenzen α - zi sind für jede Stelle unabhängig zu berechnen, weil α die höchstwertige Ziffer ist und 0 <= zi <= α . Das Borgen bei der nächst höheren Stelle, welches das schriftliche Subtrahieren kompliziert macht, entfällt hier also.
Beispiele:
| dezimal | 9999 |
|---|---|
| -768 | |
 |
9231 |
| binär | 1111 |
|---|---|
| -0110 | |
 |
1001 |
Im Fall des Binärsystems ist das (b-1)-Komplement (also das 1-Komplement) besonders einfach zu ermitteln, nämlich durch Invertierung aller Stellen.
Auch das b-Komplement erhält man ohne Subtraktion nach
Kb
Im Fall des Binärsystems invertiert man also alle Stellen und addiert an der niederwertigsten Stelle eine 1 .
Ohne weitere Kennzeichnung werden die Komplemente und die nicht negativen Zahlen in dem selben System repräsentiert. Damit man sie unterscheiden kann, werden zwei (fast) gleich große Bereiche festgelegt. Im Fall des Binärsystems sind dann alle n-Bit-Wörter, deren Ganzzahlinterpretation kleiner als bn-1 ist, eben so als nicht negative Ganzzahl zu interpretieren. Andernfalls liegt die Binärdarstellung eines Komplements vor. Dies ist hier direkt am höchstwertigen Bit zu erkennen. Das Bit wird deshalb bisweilen als Vorzeichen-Bit bezeichnet. Man vergesse aber nie, dass die folgenden Bits ein Komplement repräsentieren und nicht den Betrag der Zahl wie bei der üblichen Dezimalschreibweise.
Die Aufteilung der Interpretation von n- stelligen Repräsentationen zur Basis b wird mit der Funktion bcomplement interaktiv dargestellt. Die Basis 1 < q < 65 , die Anzahl der Stellen 0 < n <6 und die maximale positive Zahl 1 <= m können interaktiv geändert werden. Bei Änderungen von b oder n wird automatisch der übliche Wert für m eingestellt. Man könnte aber m auch anders festlegen, um z.B. den Bereich der positiven Zahlen auf Kosten der negativen zu vergrößern. Beim Binärsystem ginge dann die Interpretation des höchstwertigen Bits als Vorzeichen verloren.
Subtraktion
Die Operanden x und y seien als nicht negative Zahlen darstellbar.
Es gelte also
0 ≤ x ≤ bn-1 ; 0 ≤ y ≤ bn-1
Außerdem sei im ersten Fall x ≥ y .
Die Subtraktion z = x - y erfolgt formal durch
z = x + Kb(n)(y) = x + bn - y
Die Realisierung ist begrenzt auf n Stellen, so dass dort gilt:
z = (x + Kb(n)(y)) mod bn = x - y
Wenn x , y und x - y mit n Stellen darstellbar sind, wird das Resultat also korrekt interpretiert.
im zweiten Fall sei x < y . Dann ergibt sich
z = (x + Kb(n)(y)) mod bn = (bn - (y - x)) mod bn = Kb(n)(y - x)
Diese Realisierung der Subtraktion liefert also korrekt das b-Komplement von y - x .
Eine interaktive Demo für die Addition und Subtraktion von Zahlen in Stellen-Repräsentation unter Verwendung der Komplemente gibt
Die Addition zweier korrekt dargestellter positiver Zahlen wie auch die Addition zweier korrekt als b-Komplement dargestellter Zahlen kann ein Resultat ergeben, das im falschen Bereich liegt und damit falsch interpretiert wird. Diese Situation wird von einer richtig entworfenen Hardware des Addierers erkannt. Die Warnung wird leider häufig von der Software ignoriert. Der bislang spektakulärste Fall ist sicherlich der Absturz der ersten Ariane-5-Rakete, bei der man aus gutem Grund die bewährte alte Bord-Software laufen ließ. Allerdings wird bei der Ariane 5 deren enormer Schub (wie beim Space-Shuttle) schon wenige Sekunden nach den Start durch Schräglage des Fahrzeugs für die Beschleunigung in der horizontalen Komponente ausgenutzt. So erreichte die erste Raketenstufe korrekt geplant schon nach kurzer Zeit eine positive Horizontalkomponente der Geschwindigkeit, die bei der begrenzten Repräsentation in sämtlichen Bordrechnern in den Bereich der Komplemente lief. Das Navigationsprogramm bemerkte sofort: wir fliegen in die falsche Richtung und riss die Rakete herum, wodurch sie zu Schaden kam und gesprengt werden musste.
Eine interaktive Darstellung der Repräsentation natürlicher Zahlen im Stellensystem zur Basis 1 < b < 65 und der Operationen mit zwei Operanden liefert die Funktion inforepres . Die Graphik soll durch interaktives Spielen mit den Operanden und der Operation (+ - * div rem max min < <= > >= ) zeigen, dass das Resultat von Operationen mit in der gewählten Form (Basis und Stellenzahl) darstellbaren Operanden nicht immer auch in dieser Form darstellbar ist. Wenn die Hardware so realisiert ist, dass sie diese Situation nicht erkennt (Designfehler), oder wenn die Software die Warnungen der Hardware ignoriert (leider sehr häufiger Fall), dann ist das Resultat falsch, und zwar ohne dass dies ersichtlich ist.
Ein Beispiel für die Realisierung einer Festkomma-Arithmetik ohne Prüfung von Überläufen liefert Turbo-Pascal. Zur Demonstration dient hier ein kleines Pascal-Programm, welches der Reihe nach um Eingabe des ersten und des zweiten Operanden und dann der Operation bittet. Anschließend wird das Resultat ausgegeben (Abbruch mit 's' als Operation):
Probieren Sie z.B. folgende Operationen:
2 + 3; 100*200; 200*200; 20000 + 30000; -1 + (-32768)
Multipliziert man die natürlichen Zahlen 1 ... 10 der Reihe nach mit obigem Programm, so ergeben sich die Fakultäten:
| n | n! korrekt | n! berechnet |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 6 | 6 |
| 4 | 24 | 24 |
| 5 | 120 | 120 |
| 6 | 720 | 720 |
| 7 | 5040 | 5040 |
| 8 | 40320 | -25216 |
| 9 | 362880 | -30336 |
| 10 | 3628800 | 24320 |
Ab 8! sind sämtliche Fakultäten falsch.
Vergleichen Sie einige Additionsergebnisse von festkomm.pas mit dem Resultat der selben Rechnung mit demofixpointadd bei 16-stelliger Binärrepräsentation.