Gegeben sei eine Schaltfunktion als Ausdruck in disjunktiver Normalform, z.B.
f(a,b,c) = a'∩b'∩c'a'∩b'∩c
a'∩b∩c
a∩b∩c'
Unter Anwendung des Distributivgesetzes folgt hieraus
f(a,b,c) = a'∩b'∩(c'c)
a'∩b∩c
a∩b∩c'
oder
f(a,b,c) = a'∩b'∩c'a'∩(b'
b)∩c
a∩b∩c'
Wegen (x' 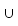 x) = 1 kann man dies weiter vereinfachen zu
x) = 1 kann man dies weiter vereinfachen zu
f(a,b,c) = a'∩b'a'∩b∩c
a∩b∩c'
bzw.
f(a,b,c) = a'∩b'∩c'a'∩c
a∩b∩c'
Tatsächlich kann man beide Zusammenfassungen zugleich vornehmen, wenn man
den Minterm, der in beiden Zusammenfassungen vorkommt doppelt schreibt unter
Ausnutzung des Gesetzes a = a 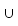 a :
a :
f(a,b,c) = a'∩b'∩c'a'∩b'∩c
a'∩b∩c
a∩b∩c'
= a'∩b'∩c' 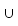 a'∩b'∩c
a'∩b'∩c 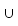 a'∩b'∩c
a'∩b'∩c 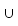 a'∩b∩c
a'∩b∩c 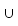 a∩b∩c'
a∩b∩c'
= a'∩b'∩(c' 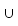 c)
c) 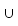 a'∩(b'
a'∩(b' 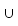 b)∩c
b)∩c 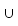 a∩b∩c'
a∩b∩c'
= a'∩b' 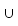 a'∩c
a'∩c 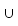 a∩b∩c'
a∩b∩c'
Das Ausklammern ist häufig bei mehr als zwei Termen möglich. Zur Vereinfachung des disjunktiven Ausdrucks kommt es, wenn die verbleibende Klammer 1 ergibt. Das ist genau dann der Fall, wenn die Klammer in ODER-Verknüpfung sämtliche 2k Bitkombinationen von den k in der Klammer vorkommenden Variablen enthält, z.B.
a'∩b'a'∩b
a∩b'
a∩b = a'∩(b'
b)
a∩(b'
b) = a'
a = 1
oder
a'∩b'∩c'a'∩b∩c'
a∩b'∩c'
a∩b∩c'
a'∩b'∩c
a'∩b∩c
a∩b'∩c
a∩b∩c
= a'∩(b'b)∩c'
a∩(b'
b)∩c'
a'∩(b'
b)∩c
a∩(b'
b)∩c
= (a'a)∩c'
(a'
a)∩c = c'
c = 1
2k Minterme, die auf diese Weise zu einem Term zusammenzufassen sind, liefern die 1 als Funktionswert für 2k Bitkombinationen der Variablen, die zusammen einen einschrittigen Code ergeben. Die Vereinfachung kann man deshalb allein aufgrund der Funktionstabelle vornehmen. Im folgenden Beispiel einer Funktionstabelle lassen sich die ersten beiden sowie die letzten vier Einspunkte jeweils zusammenfassen, da die zugehörigen Bitmuster der Variablen einen einschrittigen Code bilden:
a b c | f _______|____ 0 0 0 | 1 0 0 1 | 0 0 1 0 | 0 0 1 1 | 0 1 0 0 | 1 1 0 1 | 1 1 1 0 | 1 1 1 1 | 1
Hieraus kann man unmittelbar die disjunktive Minimalform herleiten:
f(a,b,c) = b'∩c'a
Das nach Karnaugh und Veitch benannte KV-Diagramm stellt die Funktionstabelle so dar, dass zusammenfassbare Terme benachbart sind. Das Diagramm entsteht durch ebene Darstellung eines n-dimensionalen Würfels. Die folgende Demonstration zeigt den Übergang vom dreidimensionalen Würfel zum entsprechenden KV-Diagramm.
demokvdiagram
Man beachte, dass die Nachbarschaft zyklisch ist, d.h. das äußerte linke Feld einer Zeile ist benachbart mit dem äußerten rechten Feld der selben Zeile. Das gilt entsprechend auch für Spalten.
Das Diagramm wird zusätzlich beschriftet mit allen Variablen. Balken deuten dabei an, wo die jeweilige Variable den Wert 1 hat. Die folgenden Bilder zeigen einige Beispiele für den Fall von Schaltfunktionen mit drei Variablen.
kvdiagram('(u&~v)|~w',{'u';'v';'w'})
kvdiagram([0 1 1 0 0 0 1 1],{'a';'b';'c'})
kvdiagram([1 0 1 1 0 0 1 0],{'x_1';'x_2';'x_3'})
Die Diagramme für zwei und eine Variable sind entsprechend einfacher.
kvdiagram('(u&~v)',{'u';'v'})
kvdiagram([1 0])
Im Diagramm für 4 Variable bilden die 4 Ecken einen Unterraum. Wenn die Schaltfunktion durchweg eine 1 in diesen Feldern hat, kann man den Ausdruck entsprechend vereinfachen.
kvdiagram([1 0 1 0 1 0 0 0 1 0 0 0 1 0 0 1])
Das Minimieren der disjunktiven Form erfolgt durch Festlegung von maximalen Unterräumen, in denen sämtliche Funktionswerte gleich 1 sind. Diese Unterräume dürfen sich überlappen. Die Anzahl der zur Überdeckung sämtlicher Einspunkte der Schaltfunktion erforderlichen Unterräume ist die Anzahl der in der disjunktiven Minimalform verbleibenden Terme. Die gewählten Unterräume heißen Schleifen, weil sie üblicherweise auf Papier durch Einkreisen definiert werden.
Durch Klicken auf einen Farb-Button in der Spalte "Schleifen" wird eine Schleife gewählt. Nun kann man die Zugehörigkeit von Punkten durch Anklicken ändern. Weitere Schleifen werden mit der Taste "+" erzeugt. Nach der Wahl von Schleifenmitgliedern kann man durch Klicken auf den Schleifenbutton den entsprechenden Term sichtbar machen. Mit der Taste "h" erhält man bei fokussiertem Fenster weitere Hilfe.
Minimieren Sie nun als Übung die folgenden Schaltfunktionen:
kvdiagram([0 1 1 0 0 0 1 1],{'a';'b';'c'},[4,2])
Prüfen Sie das Resultat jeweils durch Ausgabe der disjunktiven Minimalform mit der Taste "r" !
kvdiagram([1 0 0 1 1 0 0 0 1 0 1 0 1 0 1 0],{'a';'b';'c';'d'},[5,2])
kvdiagram([0 1 0 1 0 0 1 0 1 1 1 1 0 0 1 1],{'a';'b';'c';'d'},[5,3])
Die Wahl der Schleifen ist nicht eindeutig. Häufig gibt es mehrere gleichwertige Lösungen wie das folgende Beispiel zeigt:
Erste Lösung:
kvdiagram([0 1 0 1 1 1 1 0],{'a';'b';'c'},[0 0],{[2 4] [6 5] [5 7]},2)
Zweite Lösung:
kvdiagram([0 1 0 1 1 1 1 0],{'a';'b';'c'},[0 0],{[2 4] [6 2] [5 7]},2)
Die Minimierung von Schaltfunktionen mithilfe des KV-Diagramms bei mehr als 4 Variablen erfordert mehr Aufmerksamkeit, da die Nachbarschaften eines in die Ebene projizierten n-dimensionalen Würfels mit n>4 komplizierter sind:
Punkte sind benachbart, wenn sie im selben Teildiagramm benachbart sind oder in benachbarten Teildiagrammen auf den selben Positionen liegen.
Ein Beispiel mit 6 Variablen:
kvdiagram( [ 0 1 0 1 0 1 0 1 1 1 0 1 1 1 1 1 ...
0 0 0 1 1 0 1 1 0 0 1 0 1 1 1 1 ...
1 1 0 1 0 0 1 1 0 0 1 0 0 1 0 0 ...
0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1],...
{'a';'b';'c';'d';'e';'f'} , [54 15])
Eine korrekte Lösung ist:
(~a&~b&f) | (~a&c&d) | (b&~c&d&~e&~f) | (a&~b&~c&~d&~e) | (a&c&~d&e&~f) | (b&c&e&~f) | (~b&c&d&~e&f) | (a&b&~d&e&~f) | (~b&~c&e&f) | (~a&b&d&e) | (~a&~c&e&f) | (a&b&~d&~e&f) | (a&b&c&~d&~e) | (~a&~b&c&~e) | (a&b&c&e) | (a&~b&~c&d&e)