Tn sei die Menge aller Schaltfunktionen mit n Variablen und B = GF(2) der endliche Körper mit zwei Elementen und den inneren Verknüpfungen
exklusives Oder bzw. Und , die hier mit den Infixsymbolen + und * notiert
werden sollen. Wir definieren nun die Addition von Schaltfunktionen f,g,h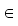 Tn
sowie das Produkt einer Schaltfunktion f
Tn
sowie das Produkt einer Schaltfunktion f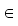 Tn mit einem Skalar λ
Tn mit einem Skalar λ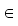 B :
B :
h = f 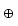 g , wo h(x) = f(x) + g(x)
g , wo h(x) = f(x) + g(x) 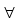 x
x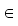 Bn
Bn
p = λ  f , wo p(x) = λ * f(x)
f , wo p(x) = λ * f(x) 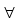 x
x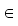 Bn
Bn
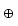 und
und  bezeichnen als Infixsymbole die neu definierten Operationen auf
der Menge Tn , + und * die inneren Verknüpfungen von B . Mit diesen
Definitionen ist die Menge Tn der Schaltfunktionen von n Variablen ein
Vektorraum. Dem Leser sei der Beweis der Axiome V1 bis V4 als Übung
empfohlen.
bezeichnen als Infixsymbole die neu definierten Operationen auf
der Menge Tn , + und * die inneren Verknüpfungen von B . Mit diesen
Definitionen ist die Menge Tn der Schaltfunktionen von n Variablen ein
Vektorraum. Dem Leser sei der Beweis der Axiome V1 bis V4 als Übung
empfohlen.
Eine Schaltfunktion f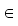 Tn , für die gilt
Tn , für die gilt
f(x) = 1 (0) für genau ein x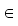 Bn und
Bn und
f(y) = 0 (1) 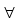 y≠x , y
y≠x , y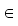 Bn
Bn
nennen wir eine Einspunktfunktion (Nullpunktfunktion) oder in anderem Zusammenhang Minterm (Maxterm).
Die folgende Tabelle stellt sämtliche Einspunktfunktionen aus dem T3 dar:
| x | b1(x) | b2(x) | b3(x) | b4(x) | b5(x) | b6(x) | b7(x) | b8(x) |
|---|---|---|---|---|---|---|---|---|
| 0 0 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 0 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 1 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 1 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 0 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 0 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 1 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 1 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Eine Einspunktfunktion lässt sich nicht als Linearkombination der anderen
Einspunktfunktionen darstellen, da diese durchweg für den Variablenvektor,
bei dem die darzustellende Einspunktfunktion gleich 1 ist, verschwinden.
Die 2n Einspunktfunktionen sind damit linear unabhängig und spannen den
Tn auf. Sie stellen also eine Basis dar. Jede Schaltfunktion f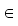 Tn lässt sich
in der Form
Tn lässt sich
in der Form
2n
f = Σ fi bi(n)
i=1
als Linearkombination der Einspunktfunktionen darstellen. Die fi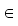 B (i=1,...,2n)
bilden den Komponentenvektor von f bezüglich der Basis der Einspunktfunktionen.
Er ist identisch mit der rechten Spalte der Funktionstabelle.
B (i=1,...,2n)
bilden den Komponentenvektor von f bezüglich der Basis der Einspunktfunktionen.
Er ist identisch mit der rechten Spalte der Funktionstabelle.