Bei der Modellierung verschiedener Problemstellungen findet man häufig sehr
ähnliche mathematische Grundstrukturen. Es lohnt sich, diese intensiv zu
untersuchen, weil man dann vieles auf das schon bekannte zurückführen kann.
Dieses Kapitel soll keine Einführung in die Algebra endlicher Mengen sein.
Vielmehr wird hier das an Mathematik zusammengestellt, was für die folgenden
Kapitel erforderlich ist. Auf Beweise wird zumeist verzichtet. In Lehrbüchern
über dieses Gebiet wird sich dem interessierten Leser eine faszinierende Welt
von Zusammenhängen eröffnen, die wir hier nicht darstellen können. Vorausgesetzt
wird hier ein Grundverständnis der Mengenlehre einschließlich solcher Begriffe
wie Relation und Abblidung sowie der Umgang mit der üblichen mathematischen
Notation.
Definition: Das kartesische Produkt zweier Mengen A und B,
in Zeichen A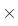 B , ist die Menge
B , ist die Menge
A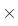 B = {(a,b) | a
B = {(a,b) | a 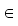 A und b
A und b 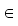 B} .
B} .
Das kartesische Produkt A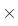 A einer Menge A mit sich bezeichnet man
kurz mit A2 .
A einer Menge A mit sich bezeichnet man
kurz mit A2 .
Definition: A sei eine Menge. Eine Abbildung f : A2 → A heißt eine innere Verknüpfung von A .
Für innere Verknüpfungen benutzt man meist die Infixnotation :
Gilt bei einer inneren Verknüpfung
dann schreibt man mit einem Verknüpfungssymbol, etwa ο , anstelle von
c = f((a,b))
auch
c = a ο b .
Neben der Präfixnotation wie z.B. bei sin(x) und der Infixnotation wie bei a + b ist für einige Operationen die Postfixnotation üblich, z.B. bei der Fakultät n! , bei der Transposition von Matrizen A' oder AT und insbesondere bei der Indizierung. Auch Programmiersprachen haben die geschichtlich gewachsenen Notationen übernommen. Ein Rechnerbefehl wie z.B.
x(3) = sin(pi/4)
enthält Postfix-, Präfix- und Infixnotation. LISP und Verwandte sind eine Ausnahme.
Verknüpfungen in der Menge der ganzen Zahlen sind die Addition und die
Multiplikation mit den üblichen Infixsymbolen + und  bzw.
bzw. 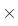 .
.
Die Subtraktion ist in der Menge der natürlichen Zahlen keine innere Verknüpfung,
wohl aber in der Menge der ganzen Zahlen. In endlichen Mengen kann man innere
Verknüpfungen durch Tabellen festlegen. Dieselbe innere Verknüpfung der
Menge {0,1} ist hier in zwei üblichen Tabellenformen angegeben:
x ο y = z y
--------|---- ο | 0 1
0 0 | 0 ---|------
0 1 | 1 x 0 | 0 1
1 0 | 0 1 | 0 0
1 1 | 0
Definition: Eine Menge mit Verknüpfungen heißt algebraische Stuktur .
Die Eigenschaften der Verknüpfungen geben der Menge ihre Struktur. Die Eigenschaften werden durch Axiome beschrieben. In der Mathematik werden Axiome einfach gesetzt und algebraische Strukturen untersucht, die ihnen genügen. In den Naturwissenschaften versucht man umgekehrt Zusammenhänge formal zu erfassen. Man findet dort häufig die bekannten algebraischen Strukturen indem man die Gültigkeit der Axiome prüft.
Definition: (A, ) und (B,
) und (B,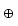 ) seien algebraische Strukturen.
) seien algebraische Strukturen.
Eine Abbildung f : A → B heißt ein Isomorphismus von
(A, ) und (B,
) und (B,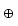 ) , wenn sie bijektiv ist und wenn
) , wenn sie bijektiv ist und wenn
f(a b) = f(a)
b) = f(a) 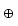 f(b)
f(b) 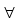 a,b
a,b 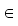 A
A
Wenn sich also herausstellt, dass eine zu untersuchende Menge mit ihren inneren Verknüpfungen isomorph zu einer bekannten Struktur ist, dann ist die Algebra übertragbar und die Untersuchung abgeschlossen. Wird für alle Elemente einer Menge auf einem Rechner eine Repräsentation gefunden und eine Realisierung der inneren Verknüpfung derart, dass der Nachweis gleicher algebraischer Struktur in der abstrakten Menge und ihrer Repräsentation gelingt, so ist die Informationstreue bewiesen.