TAMS / Java / Hades / applets (print version): contents | previous | nextCarry-select adder (8 bit)
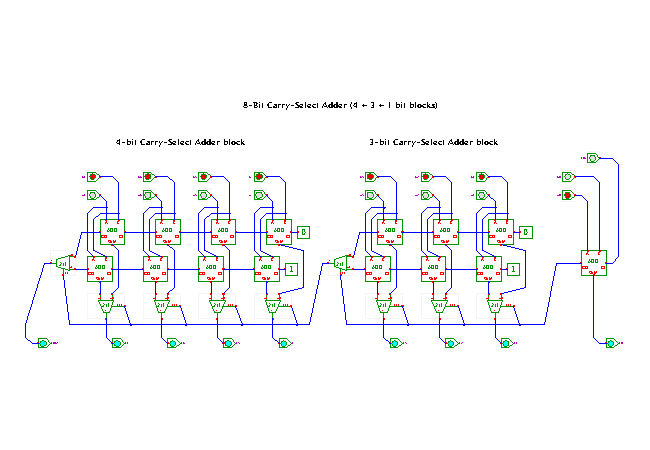 DescriptionAn 8-bit carry-select adder,
built as a cascade from a 1-bit full-adder,
a 3-bit carry-select block, and a 4-bit carry-select adder.
Click the input switches or type the 'a', 'b', 'c' bindkeys to
control the first-stage adder.
The problem of the ripple-carry adder is that each adder has to
wait for the arrival of its carry-input signal before the actual
addition can start.
The basic idea of the carry-select adder is to use blocks of
two ripple-carry adders, one of which is fed with a
constant 0 carry-in while the other is fed with a constant 1 carry-in.
Therefore, both blocks can calculate in parallel.
When the actual carry-in signal for the block arrives,
multiplexers are used to select the correct one of both precalculated
partial sums.
Also, the resulting carry-out is selected and propagated to the next
carry-select block.
In total, the carry propagation time through an n-bit adder block is
reduced from O(n) to the number of stages times the delay of the multiplexers.
Naturally, using n blocks of 1-bit carry-select adders would
incur a complexity of n multiplexers, again resulting in O(n) delay.
Therefore, a partition with (slowly) increasing block-size is chosen.
In the example, the first (least-significant) block consists of a
simple full adder,
followed by a 3-bit carry-select block,
and finally a 4-bit carry-select block.
A common choice for a 16-bit carry-select adder is to
use a 6-4-3-2-1 bit partitioning.
While the delay of the standard ripple-carry adder with n-bits is O(n),
the delay through the carry-select adder behaves as O(sqrt(n))
at a hardware cost of O(3*n).
To demonstrate this behaviour, a very large gate-delay is used for
the gates inside the 1-bit adders - resulting in an addition time
of about 0.6 seconds per adder.
The total carry-propagation time is therefore 0.6 seconds for the
first adder, and another 1.2 seconds through both carry-select blocks,
for a total of 1.8 seconds from the (A0,B0,Cin) inputs to the (Cout) output.
The longest delay path is this circuit is through the four-bit
ripple-carry block from (A4,B4) to (Cout),
for a total delay of 2.4 seconds.
Even in this (small) example, the carry-select adder is much faster
than the ripple-carry adder at 4.8 seconds.
Run the applet | Run the editor (via Webstart)
DescriptionAn 8-bit carry-select adder,
built as a cascade from a 1-bit full-adder,
a 3-bit carry-select block, and a 4-bit carry-select adder.
Click the input switches or type the 'a', 'b', 'c' bindkeys to
control the first-stage adder.
The problem of the ripple-carry adder is that each adder has to
wait for the arrival of its carry-input signal before the actual
addition can start.
The basic idea of the carry-select adder is to use blocks of
two ripple-carry adders, one of which is fed with a
constant 0 carry-in while the other is fed with a constant 1 carry-in.
Therefore, both blocks can calculate in parallel.
When the actual carry-in signal for the block arrives,
multiplexers are used to select the correct one of both precalculated
partial sums.
Also, the resulting carry-out is selected and propagated to the next
carry-select block.
In total, the carry propagation time through an n-bit adder block is
reduced from O(n) to the number of stages times the delay of the multiplexers.
Naturally, using n blocks of 1-bit carry-select adders would
incur a complexity of n multiplexers, again resulting in O(n) delay.
Therefore, a partition with (slowly) increasing block-size is chosen.
In the example, the first (least-significant) block consists of a
simple full adder,
followed by a 3-bit carry-select block,
and finally a 4-bit carry-select block.
A common choice for a 16-bit carry-select adder is to
use a 6-4-3-2-1 bit partitioning.
While the delay of the standard ripple-carry adder with n-bits is O(n),
the delay through the carry-select adder behaves as O(sqrt(n))
at a hardware cost of O(3*n).
To demonstrate this behaviour, a very large gate-delay is used for
the gates inside the 1-bit adders - resulting in an addition time
of about 0.6 seconds per adder.
The total carry-propagation time is therefore 0.6 seconds for the
first adder, and another 1.2 seconds through both carry-select blocks,
for a total of 1.8 seconds from the (A0,B0,Cin) inputs to the (Cout) output.
The longest delay path is this circuit is through the four-bit
ripple-carry block from (A4,B4) to (Cout),
for a total delay of 2.4 seconds.
Even in this (small) example, the carry-select adder is much faster
than the ripple-carry adder at 4.8 seconds.
Run the applet | Run the editor (via Webstart)
Impressum | 24.11.06
http://tams.informatik.uni-hamburg.de/applets/hades/webdemos/20-arithmetic/20-carryselect/adder_carryselect_print.html


 DescriptionAn 8-bit carry-select adder,
built as a cascade from a 1-bit full-adder,
a 3-bit carry-select block, and a 4-bit carry-select adder.
Click the input switches or type the 'a', 'b', 'c' bindkeys to
control the first-stage adder.
The problem of the ripple-carry adder is that each adder has to
wait for the arrival of its carry-input signal before the actual
addition can start.
The basic idea of the carry-select adder is to use blocks of
two ripple-carry adders, one of which is fed with a
constant 0 carry-in while the other is fed with a constant 1 carry-in.
Therefore, both blocks can calculate in parallel.
When the actual carry-in signal for the block arrives,
multiplexers are used to select the correct one of both precalculated
partial sums.
Also, the resulting carry-out is selected and propagated to the next
carry-select block.
In total, the carry propagation time through an n-bit adder block is
reduced from O(n) to the number of stages times the delay of the multiplexers.
Naturally, using n blocks of 1-bit carry-select adders would
incur a complexity of n multiplexers, again resulting in O(n) delay.
Therefore, a partition with (slowly) increasing block-size is chosen.
In the example, the first (least-significant) block consists of a
simple full adder,
followed by a 3-bit carry-select block,
and finally a 4-bit carry-select block.
A common choice for a 16-bit carry-select adder is to
use a 6-4-3-2-1 bit partitioning.
While the delay of the standard ripple-carry adder with n-bits is O(n),
the delay through the carry-select adder behaves as O(sqrt(n))
at a hardware cost of O(3*n).
To demonstrate this behaviour, a very large gate-delay is used for
the gates inside the 1-bit adders - resulting in an addition time
of about 0.6 seconds per adder.
The total carry-propagation time is therefore 0.6 seconds for the
first adder, and another 1.2 seconds through both carry-select blocks,
for a total of 1.8 seconds from the (A0,B0,Cin) inputs to the (Cout) output.
The longest delay path is this circuit is through the four-bit
ripple-carry block from (A4,B4) to (Cout),
for a total delay of 2.4 seconds.
Even in this (small) example, the carry-select adder is much faster
than the ripple-carry adder at 4.8 seconds.
Run the applet | Run the editor (via Webstart)
DescriptionAn 8-bit carry-select adder,
built as a cascade from a 1-bit full-adder,
a 3-bit carry-select block, and a 4-bit carry-select adder.
Click the input switches or type the 'a', 'b', 'c' bindkeys to
control the first-stage adder.
The problem of the ripple-carry adder is that each adder has to
wait for the arrival of its carry-input signal before the actual
addition can start.
The basic idea of the carry-select adder is to use blocks of
two ripple-carry adders, one of which is fed with a
constant 0 carry-in while the other is fed with a constant 1 carry-in.
Therefore, both blocks can calculate in parallel.
When the actual carry-in signal for the block arrives,
multiplexers are used to select the correct one of both precalculated
partial sums.
Also, the resulting carry-out is selected and propagated to the next
carry-select block.
In total, the carry propagation time through an n-bit adder block is
reduced from O(n) to the number of stages times the delay of the multiplexers.
Naturally, using n blocks of 1-bit carry-select adders would
incur a complexity of n multiplexers, again resulting in O(n) delay.
Therefore, a partition with (slowly) increasing block-size is chosen.
In the example, the first (least-significant) block consists of a
simple full adder,
followed by a 3-bit carry-select block,
and finally a 4-bit carry-select block.
A common choice for a 16-bit carry-select adder is to
use a 6-4-3-2-1 bit partitioning.
While the delay of the standard ripple-carry adder with n-bits is O(n),
the delay through the carry-select adder behaves as O(sqrt(n))
at a hardware cost of O(3*n).
To demonstrate this behaviour, a very large gate-delay is used for
the gates inside the 1-bit adders - resulting in an addition time
of about 0.6 seconds per adder.
The total carry-propagation time is therefore 0.6 seconds for the
first adder, and another 1.2 seconds through both carry-select blocks,
for a total of 1.8 seconds from the (A0,B0,Cin) inputs to the (Cout) output.
The longest delay path is this circuit is through the four-bit
ripple-carry block from (A4,B4) to (Cout),
for a total delay of 2.4 seconds.
Even in this (small) example, the carry-select adder is much faster
than the ripple-carry adder at 4.8 seconds.
Run the applet | Run the editor (via Webstart)